倍增LCA

在图论和计算机科学中，最近公共祖先（英语：lowest common ancestor）是指在一个树或者有向无环图中同时拥有v和w作为后代的最深的节点。

朴素求LCA

思想及参考代码

graph TD;
1((1)) --- 2((2))
1 --- 3((3))
3 --- 4((4))
3 --- 5((5))
4 --- 6((6))

假如在这样一棵树上，我们需要找到6和2的LCA，如何找到一个普适的流程呢。

初始化得到每一个结点的父结点编号，以及深度
将要求的两个结点较深的一个不断上移，直到两个结点深度相同
将两个结点同时一步一步地上移，直到两个结点相遇，此时所在结点即为LCA

int dep[N], fa[N];

int lca(int a, int b) {
  if (dep[a] < dep[b]) swap(a, b);
  while (dep[a] > dep[b]) a = fa[a];
  while (a != b) a = fa[a], b = fa[b];
  return a;
}

时间复杂度分析

预处理中，只需要遍历一遍树，时间复杂度为

求lca过程中，考虑树构成一条链的极端情况，此时时间复杂度为, 在查询次数多时显然是无法让人接受的。

倍增求LCA

思想

上面朴素做法最大的问题是每次只移动一步，当要移动的总步数很大时，效率就很低。

因此，能不能一次移动多步呢？

graph TD;
1((1)) --- 2((2))
1 --- 3((3))
3 --- 4((4))
3 --- 5((5))
4 --- 6((6))

我们先来声明一下，在树中，每个结点可能有多个祖先，如6的祖先有4、3、1. 我们按顺序称4是6的第一个祖先， 3是6的第二祖先，以此类推。

众所周知，任何一个正整数x转化为二进制，都可以表示为若干唯一的2的不同幂次的和，如.

假设从结果上看， a要向上移动10次，我们可以让其移动到它第八个祖先，再移动到当前结点的第二个祖先，这样就只移动了两次。

但上述的前提是，你需要记录每个结点的第个祖先是谁。

我们定义为， i号结点的第个祖先，先假设已经求出了这个数组。

同样的，定义为i号结点的深度。

此时来考虑，有了这些信息，我们怎么求出两个结点的lca。

上面的暴力算法的第一步是，将深度较大的结点上移至另一个结点的高度。

我们假设a是深度较深的， b是深度较浅的。

要跳的步数是a-b，从二进制的角度分析我们可以知道，最少的跳数，就是a-b转化为2进制后1的个数，且每种幂次只需要跳一次。

因此我们从一个上限m(大于树的最大深度)开始向下枚举，若a向上跳步后，深度不会小于b，那就往上跳；最终可以快速的到达与b相同的深度。

再来考虑，深度相同后，怎么快速的找到两个结点的最近公共祖先。

此时策略就有所不同了。

graph TD;
1((1)) --- 2((2))
1 --- 3((3))
3 --- 4((4))
3 --- 5((5))
4 --- 6((6))

以上图距离，假设要做4和5的lca，也就是3，但3的祖先也都是4和5的公共祖先，因此如果跳到3及3以上的位置，我们是不能判断这个结点是不是最近的公共祖先的。

因此我们改变策略，让此时已经同深度的a和b，跳到它们的最近公共祖先的下一层，因此我们就有明确的判断条件即两个结点跳了之后不能相同。

倍增的思路基本就是这些了，实现一下代码试试。

int lca(int a, int b) {
  if (dep[a] < dep[b]) swap(a, b);
  //跳至相同深度
  for (int i = MAX; i >= 0; i --) {
    if (dep[f[a][i]] >= dep[b]) a = f[a][i];
    if (a == b) return a;//如果b是a的祖先， 那么最终a会直接跳到b的位置
  }
  //同时往上跳
  for (int i = MAX; i >= 0; i --) {
    if (f[a][i] != f[b][i]) a = f[a][i], b = f[b][i];
  }
  //当前结点的父结点即为a和b的lca
  return f[a][0];
}

回头来考虑怎么初始化那些需要的信息。

深度dep就不用说了。

而倍增祖先数组f，则要用到一个递推的性质。

假设u的所有祖先的f信息我们都已经得到，且已知了u的父结点(f[x][0])，那么有递推式，也就是u的第个祖先是 u的第个祖先的第个祖先，并不难理解。

因此我们可以采用自顶向下的dfs来初始化f数组。

int dep[N], f[N][MAX + 1];

void dfs(int u, int fa) {
  dep[u] = dep[fa] + 1, f[u][0] = fa;
  for (int i = 1; (1 << i) <= dep[u]; i ++) f[u][i] = f[f[u][i - 1]][i - 1];
  for (auto &v : g[u]) {
    if (v != fa) dfs(v, u);
  }
}

练习

【模板】最近公共祖先（LCA）

题目描述

如题，给定一棵有根多叉树，请求出指定两个点直接最近的公共祖先。

输入格式

第一行包含三个正整数，分别表示树的结点个数、询问的个数和树根结点的序号。

接下来行每行包含两个正整数，表示结点和结点之间有一条直接连接的边（数据保证可以构成树）。

接下来行每行包含两个正整数，表示询问结点和结点的最近公共祖先。

输出格式

输出包含行，每行包含一个正整数，依次为每一个询问的结果。

样例 #1

样例输入 #1
1
2
3
4
5
6
7
8
9
10
5 5 4
3 1
2 4
5 1
1 4
2 4
3 2
3 5
1 2
4 5
样例输出 #1
1
2
3
4
5
4
4
1
4
4
提示

对于的数据，，。

对于的数据，，。

对于的数据，，，不保证 。

样例说明：

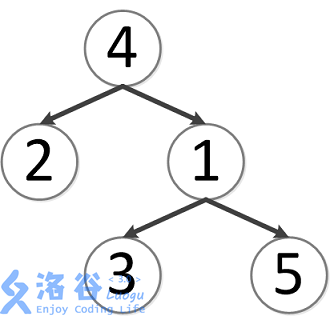
该树结构如下：

第一次询问：的最近公共祖先，故为。

第二次询问：的最近公共祖先，故为。

第三次询问：的最近公共祖先，故为。

第四次询问：的最近公共祖先，故为。

第五次询问：的最近公共祖先，故为。

故输出依次为。

2021/10/4 数据更新 @fstqwq：应要求加了两组数据卡掉了暴力跳。

注意点

结点个数最大是5e5，而是1e6多一点，所以MAX取20或19即可。
结点编号一般从1开始， 0作为根结点的父节点， 0高度为0，且0的父节点是0

参考代码

#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 10;
vector<int> g[N];
int dep[N], f[N][25];

void dfs(int u, int fa) {
  dep[u] = dep[fa] + 1, f[u][0] = fa;
  for (int i = 1; (1 << i) <= dep[u]; i ++) f[u][i] = f[f[u][i - 1]][i - 1];
  for (auto &v : g[u]) {
    if (v != fa) dfs(v, u);
  }
}

int lca(int a, int b) {
  if (dep[a] < dep[b]) swap(a, b);
  for (int i = 20; i >= 0; i --) {
    if (dep[f[a][i]] >= dep[b]) a = f[a][i];
    if (a == b) return a;
  }
  for (int i = 20; i >= 0; i --) {
    if (f[a][i] != f[b][i]) a = f[a][i], b = f[b][i];
  }
  return f[a][0];
}

int main () {
	int n, m, s; cin >> n >> m >> s;
	for (int i = 1; i < n; i ++) {
		int x, y; cin >> x >> y;
		g[x].push_back(y), g[y].push_back(x);
	}
	dfs(s, 0);
	while (m --) {
		int a, b; cin >> a >> b;
    cout << lca(a, b) << endl;
	}
	return 0;
}

参考

最低的共同祖先 - 维基百科 (wikipedia.org)

算法详解之最近公共祖先(LCA) - hulean - 博客园 (cnblogs.com)